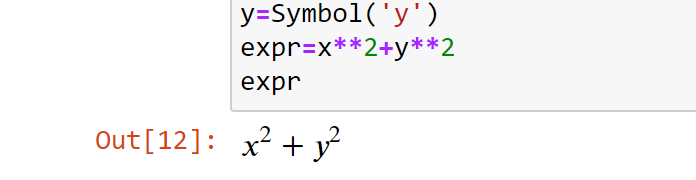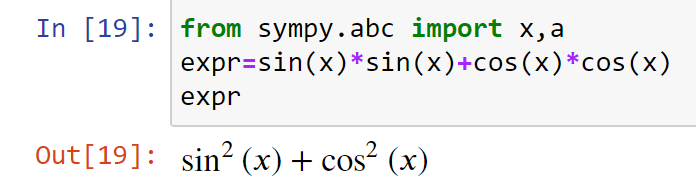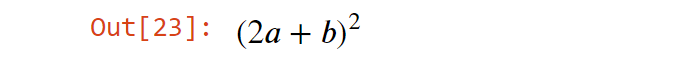символьные вычисления что это
Математическая библиотека Python SymPy
SymPy — это библиотека Python для выполнения символьных вычислений. Это система компьютерной алгебры, которая может выступать как отдельное приложение, так и в качестве библиотеки для других приложений. Поработать с ней онлайн можно на https://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать даже в интерактивном режиме.
В SymPy есть разные функции, которые применяются в сфере символьных вычислений, математического анализа, алгебры, дискретной математики, квантовой физики и так далее. SymPy может представлять результат в разных форматах: LaTeX, MathML и так далее. Распространяется библиотека по лицензии New BSD. Первыми эту библиотеку выпустили разработчики Ondřej Čertík и Aaron Meurer в 2007 году. Текущая актуальная версия библиотеки — 1.6.2.
Вот где применяется SymPy:
Установка SymPy
Такие дистрибутивы, как Anaconda, Enthough, Canopy и другие, заранее включают SymPy. Чтобы убедиться в этом, достаточно ввести в интерактивном режиме команду:
Исходный код можно найти на GitHub.
Символьные вычисления в SymPy
Символьные вычисления — это разработка алгоритмов для управления математическими выражениями и другими объектами. Такие вычисления объединяют математику и компьютерные науки для решения математических выражений с помощью математических символов.
Система компьютерной алгебры же, такая как SymPy, оценивает алгебраические выражения с помощью тех же символов, которые используются в традиционных ручных методах. Например, квадратный корень числа с помощью модуля math в Python вычисляется вот так:
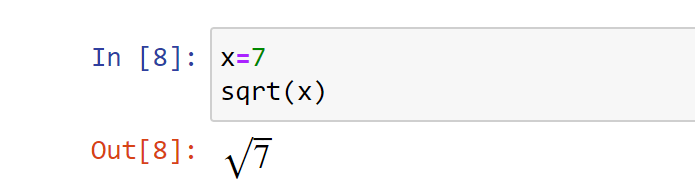
Как можно увидеть, квадратный корень числа 7 вычисляется приблизительно. Но в SymPy квадратные корни чисел, которые не являются идеальными квадратами, просто не вычисляются:
Это можно упростить и показать результат выражения символически таким вот образом:
В случае с модулем math вернется число, а вот в SymPy — формула.
Для рендеринга математических символов в формате LaTeX код SymPy, используйте Jupyter notebook:
Если выполнить эту команду в IDLE, то получится следующий результат:
Квадратный корень неидеального корня также может быть представлен в формате LaTeX с помощью привычных символов:
Символьные вычисления с помощью таких систем, как SymPy, помогают выполнять вычисления самого разного рода (производные, интегралы, пределы, решение уравнений, работа с матрицами) в символьном виде.
В пакете SymPy есть разные модули, которые помогают строить графики, выводить результат (LaTeX), заниматься физикой, статистикой, комбинаторикой, числовой теорией, геометрией, логикой и так далее.
Числа
Класс Float
Float представляет числа с плавающей точкой произвольной точности:
SymPy может конвертировать целое число или строку в число с плавающей точкой:
При конвертации к числу с плавающей точкой, также можно указать количество цифр для точности:
Для упрощения можно указать ограничение знаменателя:
Выведется дробь 1/5 вместо 3602879701896397/18014398509481984.
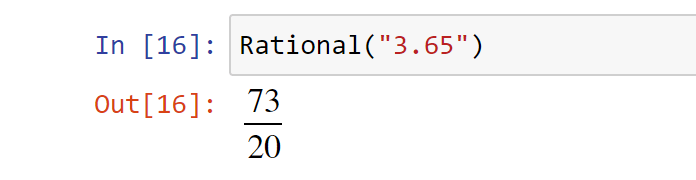
Если же в конструктор передать строку, то вернется рациональное число произвольной точности:
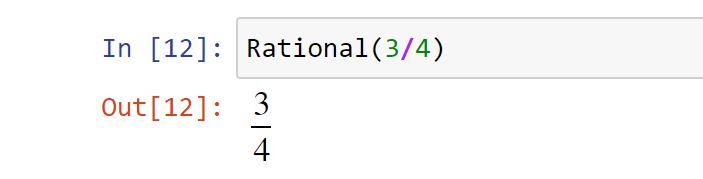
Также рациональное число можно получить, если в качестве аргументов передать два числа. Числитель и знаменатель доступны в виде свойств:
Класс Integer
Класс Integer в SymPy представляет целое число любого размера. Конструктор принимает рациональные и числа с плавающей точкой. В результате он откидывает дробную часть:
Бесконечность представлена в виде объекта-символа oo или как S.Infinity :
Символы
Аргумент функции Symbol() — это строка, содержащая символ, который можно присвоить переменной.
Код выше является эквивалентом этого выражения:
Символ может включать больше одной буквы:
В модуле abc можно найти элементы латинского и греческого алфавитов в виде символов. Таким образом вместо создания экземпляра Symbol можно использовать метод:
Смежные цифры справа берутся на 1 больше конечного значения.
Подстановка параметров
Одна из базовых операций в математических выражениях — подстановка. Функция subs() заменяет все случаи первого параметра на второй.
Этот код даст вывод, эквивалентный такому выражению.
Эта функция полезна, когда требуется вычислить определенное выражение. Например, нужно посчитать значения выражения, заменив a на 5 :
Это дает такой вывод:
Функция simplify()
Функция simplify() используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целые числа, конвертируются в SymPy.Integer и так далее. Строки также конвертируются в выражения SymPy:
Функция evalf()
Вычислим выражение с помощью evalf() и заменим r на 5:
По умолчанию точность после плавающей точки — 15, но это значение можно перезаписать до 100. Следующее выражение вычисляет, используя вплоть до 20 цифр точности:
Функция lambdify()
Функция lambdify() переводит выражения SymPy в функции Python. Если выражение, которое нужно вычислить, затрагивает диапазон значений, то функция evalf() становится неэффективной. Функция lambdify действует как лямбда-функция с тем исключением, что она конвертирует SymPy в имена данной числовой библиотеки, обычно NumPy. По умолчанию же она реализована на основе стандартной библиотеки math.
У выражения может быть больше одной переменной. В таком случае первым аргументом функции является список переменных, а после него — само выражение:
Логические выражения
Запросы
Следующие свойства предоставляют полезную информацию о выражении:
algebraic(x)
Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 — это решение x2 − 2 = 0. Следовательно, это выражения является алгебраическим.
complex(x)
Предикат комплексного числа. Является истиной тогда и только тогда, когда x принадлежит множеству комплексных чисел.
composite(x)
Предикат составного числа, возвращаемый ask(Q.composite(x)) является истиной тогда и только тогда, когда x — это положительное число, имеющее как минимум один положительный делитель, кроме 1 и самого числа.
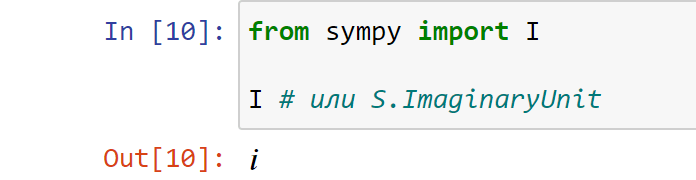
imaginary
Свойство представляет предикат мнимого числа. Является истиной, если x можно записать как действительное число, умноженное на мнимую единицу.
rational, irrational
Q.irrational(x) истинно тогда и только тогда, когда x — это любое реальное число, которое нельзя представить как отношение целых чисел. Например, pi — это иррациональное число.
positive, negative
Предикаты для проверки того, является ли число положительным или отрицательным.
zero, nonzero
Предикат для проверки того, является ли число нулем или нет.
Что такое символические вычисления?
в математике и информатике, компьютерной алгебре, также называемой символическое вычисление или алгебраическое вычисление-научная область что относится к изучению и разработке алгоритмов и программного обеспечения для манипулирования математическими выражениями и другими математическими объекты
фокусируется ли символическое вычисление на манипуляции символами и вычислениях? Программа Lisp написана в виде АСТ с атомами как листьями. Lisp считается языком для символьных вычислений. Означает ли это, что в символическом вычислении это:
по данным этот вопрос, напротив символического вычисления числовых вычислений. В чем основная разница между этими двумя? Когда я работаю с Октавой (я изучаю ее), мне приходится много работать с числами и угадывать значение эти магические числа много раз. Это фокус численных вычислений?
5 ответов
примеры символических выражений:
теперь задача будет состоять в том, чтобы создать хороший план, который забирает все посылки
в приведенных выше примерах символы обозначают места и вещи (грузовик, посылка). Символьные выражения описывают ситуацию, генератор плана возвращает последовательность действия-снова описываются как символические выражения.
символическое вычисление-это то, что подчеркивает термин рерайтинг над оценка (e-value-ation, извлечение значения). символы (также называемый выражения) перезаписываемые термины значения подразумевают потерю или конец перезаписываемости. В каком-то смысле символы более абстрактны, а ценности более конкретны.
и, конечно, есть также противоположный случай уравнений, настолько неразрешимых для перезаписи, что они могут только приблизительно ответить с помощью численных методов.
символьные вычисления всегда точны (бесконечная точность). В числовых вычислениях точность конечна
вы можете посмотреть книгу «нежное введение в вычисление symbloc» как http://www.cs.cmu.edu /
dst / LispBook. Шепелявый диалект-обычный шепелявый.
Это больше похоже на вашу третью догадку, но тогда я тоже новичок.
Символьные вычисления средствами Python. Часть1. Основы
При решении задач математического моделирования процессов и объектов часто очень практично использовать алгоритмы на языке Python с использованием символьных вычислений. Основываясь на библиотеке SymPy, Python с успехом справляется с решением уравнений и систем, интегрированием и дифференцированием, вычислением пределов, разложением в ряд и суммированием рядов, упрощением выражений, выполняет поиск решения дифференциальных уравнений и систем.
При использовании символьных вычислений пользователю предоставляется возможность управлять работой программы в процессе ее исполнения путём ввода любых допустимых функций с заданным количеством переменных.
Как преподаватель дисциплины «Компьютерная техника и программирование», в модуле, посвященном программированию на языке Python, я знакомлю студентов с возможностями этого языка для научных исследований. Вашему вниманию представляется цикл статей, в которых можно ознакомиться с символьными вычислениями на Python. Хочу сразу предупредить, что данные статьи не претендуют на абсолютную уникальность, так как собраны на основании материалов из различных источников, их цель – обучить студентов основам символьных вычислений.
Самым первым шагом на пути к символьным вычислениям является импортирование функций модуля SymPy с помощью pip, системы управления пакетами Python. Если вы с этим справились, сразу перейдем к объявлению переменных.
Примечание. Для сокращения записи во всех следующих примерах не приводится первая строка: from sympy import *
Явное объявление символьных переменных
Для символьных вычислений с помощью модуля SymPy символьные переменные и функции должны быть объявлены как таковые. В программах для математических вычислений, таких как Mathematica или Maple, переменные сразу рассматриваются как символьные. В Python же их необходимо принудительно объявить символьными, и сделать это можно несколькими путями. Самым простым будет использование функций symbols() или var(). Первая функция возвращает ссылку на символьный объект в виде какой-либо переменной. Вторая, без присваивания создает символьную переменную.
Главное отличие между функциями symbols() и var() состоит в том, первая функция возвращает ссылку на символьный объект. Для использования в дальнейшем, ее нужно присвоить какой-либо переменной. Вторая, без присваивания, создает символьную переменную.
В функциях symbols() и var() можно объявлять символьные переменные с индексом:
Также можно назначить тип и накладывать ограничения на символьные переменные прямо в функциях symbols() и var(). Иногда без таких ограничений очевидные преобразования не работают, например, сравните:
Чтобы создать контейнер для одиночного символа, используем аргумент seq=True:
Определение действительных значений для символьных переменных:
Функция S()
Иногда символьные выражения могут быть проинтерпретированы как числовые константы Python, а не SymPy. Поэтому для объявления символьных переменных, а также для преобразования числовых констант в символьные, применяют функцию S(), например, сравним:
Разница между постоянной Python и символьной состоит в том, что символьная константа может быть вычислена с заданной степенью точности, как показано в следующем примере в сравнении со стандартной функцией round():
Cимвольные имена
Если в текущей сессии необходимо использовать символьную математику постоянно, то можно импортировать общепринятые символьные имена из модуля sympy.abc:
Имя переменной из пространства имен можно удалить командой del имя1, имя2. :
Для восстановления значений стандартных констант, а также имен некоторых функций, нужно повторно загрузить модуль sympy.
Метод subs(. )
Следует помнить, что при записи символьного выражения может автоматически выполняться его упрощение, например:
Метод subs(. ) используется для вычисления символьного выражения при заданных значениях переменных, например:
Если в методе subs использовать два аргумента, то они интерпретируются как subs(old,new), т.е. старый идентификатор old заменяется новым new. Аргумент метода subs() может быть последовательностью, которая должна содержать пары (old,new), а может быть символьным выражением, например:
Обратим ваше внимание на следующую особенность работы с переменными (символьными и обычными переменными Python). Выполним следующий код:
Здесь действует правило: если переменная изменилась, то созданное ранее выражение, содержащее эту переменную, не пересчитывается автоматически. Это правило срабатывает и для обычных переменных Python.
Операции с дробями
Модуль SymPy может проводить вычисления с дробями и приводить их к общему знаменателю, например, сравните:
Функции Rational(числитель, знаменатель) и Integer(. ) используются для создания рациональных дробей без десятичного округления:
Округления вычислений
В символьных вычислениях работает правило – если ничего не сказано, не делать никаких округлений. Посмотрите, как в первом случае Python преобразует выражение, но оставит в записи ответа квадратный корень и не выполнит никаких округлений, а во втором, так как одно из чисел задано с десятичной точкой, результат будет приближенным:
Для любого символьного объекта существует метод evalf(. )(evaluate float), который возвращает его десятичное представление:
В методе evalf([n. ]) можно использовать аргумент, задающий точность результата (n = количество значащих цифр)
Также всегда нужно помнить, что вещественная арифметика не возвращает точный результат, сравните:
Если известно, что результат содержит погрешность вычислений, то с помощью опции chop=True метода evalf() ее можно удалить. Очень маленькое значение вещественной или мнимой части результата в этом случае заменяется нулем. Возьмем предыдущий пример:
Бесконечность
После выполнения первой строки from sympy import * становится доступен символ бесконечности – oo (две буквы „o‟), с которым тоже можно выполнять определенные операции:
Символ бесконечности в основном используется функциями limit() и integrate() при задании пределов интегрирования, о чем мы поговорим в одной из следующих статей.
Вывод
Рассмотренные в статье символьные вычисления отличаются от числовых методов тем, что результаты можно и дальше исследовать, например, определять экстремумы функций, решать уравнения со вложенными переменными и так далее.
Надеюсь, моя статья будет полезна всем интересующимся программированием на языке Python, студентам и тем, кто занимается научными исследованиями.
Символьные вычисления
Компьютерная алгебра (в отличие от численных методов) занимается разработкой и реализацией аналитических методов решения математических задач на компьютере и предполагает, что исходные данные, как и результаты решения, сформулированы в аналитическом (символьном) виде.
При анализе математической модели результатом могут быть общие и частные аналитические решения сформулированной математической задачи и их интерпретации.
Аналитические решения чаще удаётся получить для наиболее грубых (простых) моделей, реже — для более точных, сложных (нужно использовать численные методы, позволяющие получить частные численные решения многих задач).
Связанные понятия
Теория комбинаторных схем — это часть комбинаторики (раздела математики), рассматривающая существование, построение и свойства семейств конечных множеств, структура которых удовлетворяет обобщённым концепциям равновесия и/или симметрии. Эти концепции не определены точно, так что объекты широкого диапазона могут пониматься как комбинаторные схемы. Так, в одном случае комбинаторные схемы могут представлять собой пересечения множеств чисел, как в блок-схемах, а в другом случае могут отражать расположение.
В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.
Прострáнством называется математическое множество, имеющее структуру, определяемую аксиоматикой свойств его элементов (например, точек в геометрии, векторов в линейной алгебре, событий в теории вероятностей и так далее).Подмножество пространства называется «подпространством», если структура пространства индуцирует на этом подмножестве структуру такого же типа (точное определение зависит от типа пространства).
В теории алгоритмов классами сложности называются множества вычислительных задач, примерно одинаковых по сложности вычисления. Говоря более узко, классы сложности — это множества предикатов (функций, получающих на вход слово и возвращающих ответ 0 или 1), использующих для вычисления примерно одинаковые количества ресурсов.
Библиотека Sympy: символьные вычисления в Python
Документацию и исходный код этой библиотеки можно найти на ее официальной странице.
Первые шаги с SymPy
Используем SymPy как обычный калькулятор
Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.
Символы
В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:
После их задания, с ними можно производить различные манипуляции.
Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:
Алгебраические преобразования
SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.
Раскрытие скобок
Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:
При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.
Упрощение выражений
Вычисления
Вычисления пределов
Также можно вычислять пределы, которые стремятся к бесконечности.
Дифференцирование
Проверим результат последней функции при помощи определения производной через предел.
tan 2 (𝑥)+1 Результат тот же.
Разложение в ряд
Интегрирование
Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:
Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.
Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).
Решение уравнений
Системы линейных уравнений
Факторизация
Булевы уравнения
Линейная алгебра
Матрицы
Матрицы в SymPy создаются как экземпляры класса Matrix :
И производить с ними разные манипуляции:
Дифференциальные уравнения
Теперь решим следующее дифференциальное уравнение: