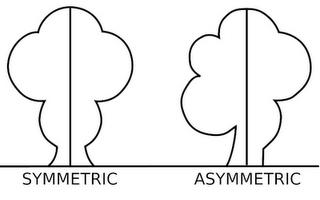
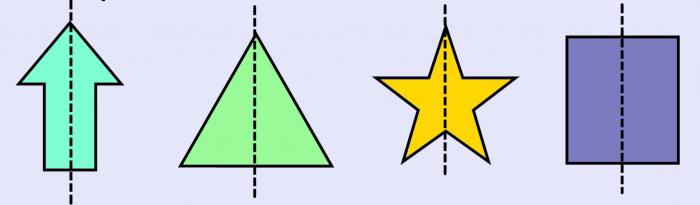
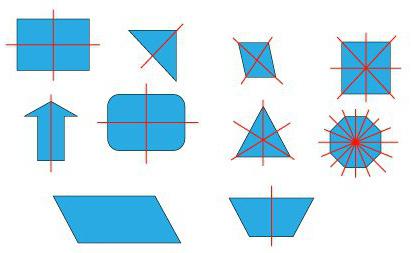
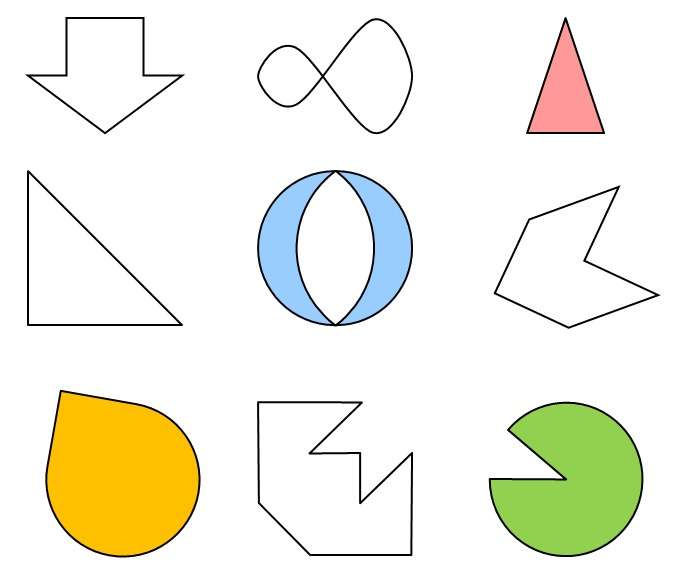
симметричные многоугольники 2 класс что это такое
Что такое симметрия и асимметрия?
Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?
Что означает симметрия в разных науках?
Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.
Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.
Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.
Как определяют симметрию разные словари?
На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.
В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.
Когда говорят об асимметрии?
Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.
В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.
О центральной и осевой симметрии
В математике выделяют такие ее виды:
Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.
В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.
Какие фигуры являются симметричными?
Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.
Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.
Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.
Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.
К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.
Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.
У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.
Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.
Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.
Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями
Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.
Общие сведения
Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.
Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.
Любого вида многоугольник состоит из следующих частей:
Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.
Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.
Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.
А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.

Простейшие четырёхугольники
Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.
Наиболее часто приходится сталкиваться со следующими видами:
Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.
Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.
Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.

Треугольный многоугольник
Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.
В зависимости от особенностей, фигура может называться:
Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.
Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.
Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.
Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.

Теорема об углах
Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.
Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.

Симметрия

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
Вывод
«Эти симметричные фигуры» (2 класс)
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Урок по математике на тему: «Эти симметричные фигуры…» Подготовлен и проведен учителем начальных классов Фалюта Л.В. во 2«А» классе
Ну-ка, проверь, дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка?
Запомните: фигурки, у которых одна половинка как две капли похожа на другую, называют зеркальной симметрией. (ОСЕВОЙ)
Эти фигуры называют симметричными относительно прямой линии, а прямую линию называют осью симметрии.
Достройте вторую половинку нашей работы.
Симметричен человек И увидеть можно: Глаза два и уха два. И руки две- точно! Две ноги и две ноздри, Щечки улыбаются. Симметричен человек, Это всех касается!
Издревле люди стремились украсить все, что окружало их в быту. Они старались простой предмет сделать нарядным, внести праздничность в повседневную жизнь. Украшали дома и ворота, столы и сундуки, орудия труда, посуду и многое другое.
Природа вдохновила человека на создание симметричных форм. Они придумывали удивительные замысловатые орнаменты. В построении орнамента часто используется симметрия. Сегодня на уроке мы будем учиться создавать орнаменты из геометрических фигур с помощью симметрии. СУРПАН- головная повязка
Орнамент – это узор, элементы которого подчинены определенному ритму
Красный – свобода Желтый – цвет солнца Белый – чистота помыслов, честь, благородство
Симметрия – порядок, четкость в изображении
Симметрия – способ создания красоты
Симметрия – способ создания совершенства
Симметрия! Я гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, ты в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза.
Выставка работ учащихся.
http://nikolaeva.21204s01.edusite.ru/p8aa1.html чувашская вышивка http://silova.21411s16.edusite.ru/p26aa1.html чувашская вышивка http://www.bestreferat.ru/referat-113224.html чувашские узоры http://artmus.culture21.ru/ppage.aspx?objid=23031&page=943&type=14&auth=1137&norole=1 чувашский орнамент www.chuvbook.ru учебник чувашского языка, рабочая тетрадь для 2 класс Картинки-раскраски
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-674766
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения разработает внеучебные курсы для школьников
Время чтения: 1 минута
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
Трехлетнюю олимпиаду среди школ запустят в России в 2022 году
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Псковских школьников отправили на дистанционку до 10 декабря
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
«Урок с использованием ИКТ» во 2-м классе по теме «Симметрия»
Тема урока: «Симметрия».
Тип урока: урок с применение ИКТ.
Вид: комбинированный.
План урока:
| Содержание этапов урока | Виды и формы работы |
| 1. Организационный момент | Приветствие |
| 2. Мотивационное начало урока | Постановка цели урока |
| 3. Объяснение темы урока | Использование опорного конспекта и презентации |
| 4. Этап обобщения, систематизации знаний и закрепление изученного | Работа в печатных тетрадях, выполнение заданий |
| 5. Практическая работа на ПК | Работа с программой, задание: «Дорисуй платок» |
| 6. Подведение итогов, домашнее задание | Нарисовать домик, симметричный относительно вертикальной оси, на отдельном тетрадном листочке в клеточку. |
I. Организационный момент
II. Мотивационное начало урока
Учитель: Здравствуйте! Тема нашего сегодняшнего урока: «Симметрия».
Цель нашего урока – выяснить, что такое симметрия, где в жизни мы с ней встречаемся?
Для достижения цели нашего урока мы воспользуемся рисунками, которые лежат на ваших столах в конвертиках, такие же рисунки мы рассмотрим на экране (Приложение 1)
– Посмотрите на геометрические фигуры, назовите их.
– Возьмите первую фигуру и согните её пополам. Точно так же согните все фигуры.
– А теперь разверните рисунки, у вас получились две одинаковые фигуры, которые разделяет линия сгиба.
– Линия сгиба, называется осью симметрии.
Игра «Зеркало»
Учитель предлагает ученикам встать и стать его зеркалом, т.е. повторять все его движения в зеркальном отражении. Учитель поднимает руку – ученики тоже, отставляет ногу в сторону – ученики тоже. Однако нужно напомнить ученикам, что они – зеркало, т.е. они должны отражать все движения учителя. Возможно, дети поднимут вместе с правой рукой учителя свою правую руку (как на физкультуре), но, отражаясь в зеркале, правая рука становится левой. А если приблизиться к зеркалу вплотную, то можно слиться со своим отражением. Для демонстрации этого можно поставить перед собой какого-либо ученика, а затем медленно поднимать вверх свою правую руку, держа его левую. После этого провести еще ряд упражнений.
Теперь мы знаем, что в зеркале все становится наоборот: правая рука станет левой, левая нога – правой.
III. Объяснение нового материала
Учитель: Посмотрите теперь все на экран.
– Это предметы окружающей нас среды, назовите, что вы видите? (Слайд 2)
(Дети называют предметы)
– А теперь внимательно посмотрите на бабочку, крылья у бабочки одинаковые,
т.е. симметричные. назовите ещё симметричные предметы. (Слайды 2, 3)
– Из конверта возьмите рисунок 1 (Слайд 4) и раскрасьте симметричные предметы.
Учитель: Теперь давайте выполним задание 44 из тетради (Слайд 5) Представим себе, что на линию АБ поставили зеркало. Что мы увидим в этом зеркале? (Отражение этих предметов.) А как изменятся в этом зеркале предметы? (Будет все наоборот: то, что было правым – станет левым и наоборот.) Говорят, что эти отражения симметричны самим предметам.
После этого дети находят пары симметричных фигур: кораблики и варежки. А домики и уточки не будут симметричны.
Это можно проверить, если сложить лист по линии АБ. В этом случае предметы должны совпасть. Такие предметы называются симметричными относительно оси АБ.
IV. Этап обобщения, систематизации знаний и закрепление изученного
Учитель: А теперь мы будем учиться строить фигуры, которые симметричны данным относительно заданной оси. (Cлайд 6)
а) Далее, учитель объясняет детям, как получить точку, симметричную данной относительно заданной оси: нужно отступить от оси направо на столько же клеточек, на сколько отстоит исходная точка.
Аналогично нужно получить концы отрезка, или вершины треугольника, или точки, ограничивающие и определяющие флажок. Затем полученные точки нужно соединить по линейке и образовать искомые фигуры. И, чтобы убедиться в их симметричности относительно данным фигурам, – сложить лист по прямой АБ.
Учитель: Эта прямая называется вертикальной осью симметрии, а теперь попробуем нарисовать фигуры, симметричные относительно горизонтальной оси.
– Показывая разные фигуры и предметы (квадрат, треугольник, домик, солнышко и т.д.) учитель спрашивает ребят наличие или отсутствие осей симметрии.
К доске вызываются три ученика, с каждого ряда по одному ученику, и работают у доски с рисунками (дерево, груша и стрекоза), т.е. проводят оси симметрии у предметов, остальные ребята на местах выполняют задание (рисунок 3) из конверта.
Задание 47 выполняется в тетради самостоятельно (Cлайд 7)
Физкультминутка
На раз — всем дружненько присесть.
На два — подняться — руки вверх.
На три — носки свои достать.
И за парты сесть опять.
– Ну вот мы уже хорошо научились рисовать, поэтому возьмите из конверта заготовки рисунка «львёнка», дорисуйте по клеткам и раскрасьте его так, чтобы он был симметричным не только по форме, но и по цвету.
Загадки, задачи-шутки
1) Мудрец в нем видел мудреца,
Глупец – глупца,
Баран – барана,
Овцу в нем видела овца,
И обезьяну – обезьяна,
Но вот подвели к нему Федю Баратова,
И Федя увидел неряху лохматого. (Зеркало.)
2) Два конца, два кольца, а посередине – гвоздик. (Ножницы.)
А есть ось симметрии? (Да. В случае непонимания – показать ножницы, но симметричные, или изобразить на доске.)
3) Между двух светил я в середине один. (Нос.)
А есть ли ось симметрии? (Да.)
4) Какие буквы имеют оси симметрии? (Слайд 11)
(А, В, Д, Е, Ж, 3, К, Л, М, Н, О, П, С, Т, Ф, X, Ш, Э, при этом имеется в виду их симметричное написание. Выписать их на доске.)
Какие из них имеют несколько осей симметрии? (Ж – 2 оси, Н –2 оси, О – много, X– 2 оси.)
V. Практическая работа на ПК
Программа дорисуй платок относительно оси.
VI. Домашнее задание.
а) Нарисовать домик, симметричный относительно вертикальной оси, на отдельном тетрадном листочке в клеточку.
б) Принести два тетрадных листочка.