с чем совпадают высоты квадрата

Квадрат

Квадрат – ромб, у которого все углы прямые.

Квадрат – прямоугольник с равными сторонами.

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Свойства квадрата

Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Описанная окружность

Около квадрата можно описать окружность. Сторона и радиус окружности связаны соотношением:

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:

Площадь квадрата

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

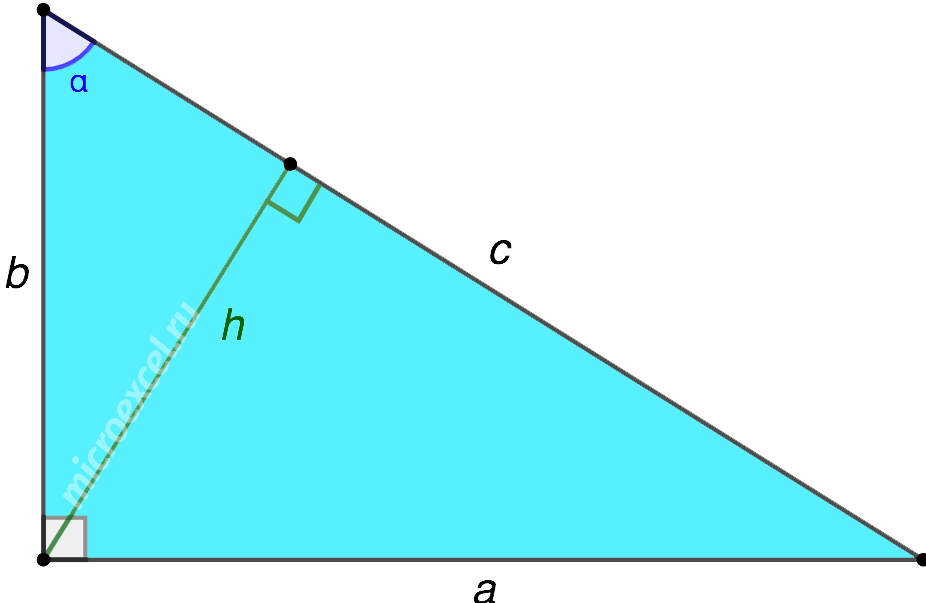
Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

3. △ABD ∼ △ADC по двум равным углам: ∠ABD = ∠DAC, ∠BAD = ∠ACD.
Доказательство: ∠BAD = 90° – ∠ABD (ABC). В то же время ∠ACD (ACB) = 90° – ∠ABC. Следовательно, ∠BAD = ∠ACD.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

Источник

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Очевидно, радиус окружности равен половине диагонали квадрата.

Диаметр окружности равен стороне квадрата.

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.

Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Источник

Определите, можете ли вы использовать тригонометрию, чтобы найти высоту квадрата. Вы можете использовать тригонометрию, только если у вас есть измерение длины для диагональной линии, которое может разделить квадрат на два равных треугольника. Вам нужно три части информации, чтобы использовать тригонометрию. Любая комбинация трех углов или сторон поможет вам найти другие недостающие измерения для оставшихся углов или сторон. Два исключения имеют только три измерения угла или только один угол и две стороны.

Определите, какие части информации у вас есть. Если у вас есть длина диагональной линии, вы сможете определить высоту квадрата. Зная, что квадраты имеют четыре прямых угла, у вас также есть два угла для использования. Диагональная линия разрезает прямой угол на два равных угла, половина правильного угла. Это 45 градусов.

Установите свое уравнение, где «h» равно неизвестной высоте квадрата, а гипотенуза равна 50. Косинус (45 градусов) = h / 50.

Используйте алгебру, чтобы найти неизвестное «ч». Умножьте обе стороны на 50, чтобы выделить «h» в правой части уравнения. Это меняет 50 на «ч». Теперь у вас есть 35, 35 = h, где диагональная линия равна 50. Высота квадрата составляет 35, 35. Используйте единицы измерения, в которых указана длина диагональной линии. Это могут быть сантиметры, дюймы или футы.

подсказки

Вы также можете измерить высоту квадрата, если он имеет правильный размер.

Как найти высоту треугольника

Как преобразовать наклонную высоту в обычную высоту

Как найти высоту трапеции

Поскольку высота трапеции обычно не лежит вдоль края фигуры, у учеников возникает проблема с определением точной высоты. Изучив геометрическое уравнение, которое связывает площадь трапеции с ее основаниями и высотой, вы можете сыграть некоторую алгебраическую перетасовку, чтобы напрямую рассчитать высоту.

Источник

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

Из равенства (1) найдем d:

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

Из формулы (5) найдем R:

или, умножая числитель и знаменатель на , получим:

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

Эти реугольники также равнобедренные. Тогда

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Источник