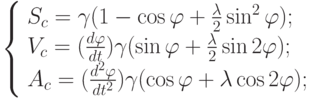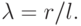С чего начинается построение математической модели
Особенности построения математических моделей
Для построения математической модели необходимо:
Математическое описание исследуемых процессов и систем зависит от:
На этапе выбора математической модели устанавливаются: линейность и нелинейность объекта, процесса или системы, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса. При математическом моделировании сознательно отвлекаются от конкретной физической природы объектов, процессов или систем и, в основном, сосредотачиваются на изучении количественных зависимостей между величинами, описывающими эти процессы.
Построение математической модели обычно начинается с построения и анализа простейшей, наиболее грубой математической модели рассматриваемого объекта, процесса или системы. В дальнейшем, в случае необходимости, модель уточняется, делается ее соответствие объекту более полным.
Возьмем простой пример. Нужно определить площадь поверхности письменного стола. Обычно для этого измеряют его длину и ширину, а затем перемножают полученные числа. Такая элементарная процедура фактически обозначает следующее: реальный объект (поверхность стола) заменяется абстрактной математической моделью – прямоугольником. Прямоугольнику приписываются размеры, полученные в результате измерения длины и ширины поверхности стола, и площадь такого прямоугольника приближенно принимается за искомую площадь стола.
С помощью этого простого примера было показано, что математическая модель не определяется однозначно исследуемым объектом, процессом или системой. Для одного и того же стола мы можем принять либо модель прямоугольника, либо более сложную модель четырехугольника общего вида, либо четырехугольника с закругленными углами. Выбор той или иной модели определяется требованием точности. С повышением точности модель приходится усложнять, учитывая новые и новые особенности изучаемого объекта, процесса или системы.
Рассмотрим другой пример: исследование движения кривошипно-шатунного механизма (Рис. 2.1).
Для кинематического анализа этого механизма, прежде всего, необходимо построить его кинематическую модель. Для этого:
Запишем эти уравнения:
где С0 – крайнее правое положение ползуна С:
r – радиус кривошипа AB;
l – длина шатуна BC;

Полученные трансцендентные уравнения представляют математическую модель движения плоского аксиального кривошипно-шатунного механизма, основанную на следующих упрощающих предположениях:
Таким образом, важно еще раз подчеркнуть, что, чем выше требования к точности результатов решения задачи, тем больше необходимость учитывать при построении математической модели особенности изучаемого объекта, процесса или системы. Однако, здесь важно во время остановиться, так как сложная математическая модель может превратиться в трудно разрешимую задачу.
Наиболее просто строится модель, когда хорошо известны законы, определяющие поведение и свойства объекта, процесса или системы, и имеется большой практический опыт их применения.
Более сложная ситуация возникает тогда, когда наши знания об изучаемом объекте, процессе или системе недостаточны. В этом случае при построении математической модели приходится делать дополнительные предположения, которые носят характер гипотез, такая модель называется гипотетической. Выводы, полученные в результате исследования такой гипотетической модели, носят условный характер. Для проверки выводов необходимо сопоставить результаты исследования модели на ЭВМ с результатами натурного эксперимента. Таким образом, вопрос применимости некоторой математической модели к изучению рассматриваемого объекта, процесса или системы не является математическим вопросом и не может быть решен математическими методами.
Основным критерием истинности является эксперимент, практика в самом широком смысле этого слова.
Построение математической модели в прикладных задачах – один из наиболее сложных и ответственных этапов работы. Опыт показывает, что во многих случаях правильно выбрать модель – значит решить проблему более, чем наполовину. Трудность данного этапа состоит в том, что он требует соединения математических и специальных знаний. Поэтому очень важно, чтобы при решении прикладных задач математики обладали специальными знаниями об объекте, а их партнеры, специалисты, – определенной математической культурой, опытом исследования в своей области, знанием ЭВМ и программирования.
Математическое моделирование и процесс создания математической модели
1. Математическое моделирование
и процесс создания математической модели.
Математическое моделирование представляет собой метод исследования объектов и процессов реального мира с помощью их приближенных описаний на языке математики — математических моделей.
Процесс создания математической модели условно можно разбить на ряд основных этапов:
1) построение математической модели;
2) постановка, исследование и решение соответствующих вычислительных задач;
3) проверка качества модели на практике и модификация модели.
Рассмотрим основное содержание этих этапов.
Построение математической модели. Математической моделью называется аналитическое выражение, которое находится в результате анализа некой физической системы или явления, включающей в себя несколько неизвестных параметров этой системы или явления, подлежащих определению на основе данных эксперимента. С помощью наблюдений и экспериментов, практики выявляются основные «характеристики» явления, которым сопоставляются некоторые величины. Как правило, эти величины принимают числовые значения, т. е. являются переменными, векторами, матрицами, функциями и т. д.
Установленным внутренним связям между «характеристиками» явления придается форма равенств, неравенств, уравнений и логических структур, связывающих величины, включенные в математическую модель. Таким образом, математическая модель становится записью на языке математики законов природы.
Подчеркнем, что математическая модель неизбежно представляет собой компромисс между бесконечной сложностью изучаемого явления и желаемой простотой его описания.
Математические модели часто разделяют на статические и динамические. Статическая модель описывает явление или ситуацию в предположении их завершенности, неизменности (т. е. в статике). Динамическая модель описывает, как протекает явление или изменяется ситуация от одного состояния к другому (т. е. в динамике). При использовании динамических моделей, как правило, задают начальное состояние системы, а затем исследуют изменение этого состояния во времени. В динамических моделях искомое решение часто является функцией времени у=у(t), переменная t в таких моделях, как правило, бывает выделенной и играет особую роль.
Постановка, исследование и решение вычислительных задач. Для того чтобы найти интересующие исследователя значения величин или выяснить характер из зависимости от других входящих в математическую модель величин, ставят, а затем решают математические задачи.
Выявим основные типы решаемых задач. Для этого все величины, включенные в математическую модель, условно разобьем на три группы:
1) исходные (входные) данные х,
2) параметры модели a,
3) искомое решение (выходные данные) у.
1). Наиболее часто решают так называемые прямые задачи, постановка которых выглядит следующим образом: по данному значению входного данного х при фиксированных значениях параметров a требуется найти решение у. Процесс решения прямой задачи можно рассматривать как математическое моделирование причинно-следственной связи, присущей явлению. Тогда входное данное х характеризует «причины» явления, которые задаются и варьируются в процессе исследования, а искомое решение у — «следствие».
Для того чтобы математическое описание было применимо не к единичному явлению, а к широкому кругу близких по природе явлений, в действительности строят не единичную математическую модель, а некоторое параметрическое семейство моделей. Выбор конкретной модели из этого семейства осуществляется фиксацией значений параметров модели a. Например, в роли таких параметров могут выступать некоторые из коэффициентов, входящих в уравнения.
2). Большую роль играет решение так называемых обратных задач, состоящих в определении входного данного х по данному значению у (параметры модели a, как и в прямой задаче, фиксированы). Решение обратной задачи — это в определенном смысле попытка выяснить, какие «причины» x привели к известному «следствию» у. Как правило, обратные задачи оказываются сложнее для решения, чем прямые.
3). Помимо двух рассмотренных типов задач следует упомянуть еще один тип — задачи идентификации. В широком смысле задача идентификации модели — это задача выбора среди множества всевозможных моделей той, которая наилучшим образом описывает изучаемое явление. В такой постановке эта задача выглядит как практически неразрешимая проблема. Чаще задачу идентификации понимают в узком смысле, как задачу выбора из заданного параметрического семейства моделей конкретной математической модели (с помощью выбора ее параметров a), с тем чтобы оптимальным в смысле некоторого критерия образом согласовать следствия из модели с результатами наблюдений.
Указанные три типа задач (прямые, обратные и задачи идентификации) будем называть вычислительными задачами. Для удобства изложения в дальнейшем независимо от типа решаемой задачи будем называть набор подлежащих определению величин искомым решением и обозначать через у, а набор величин — входным данным и обозначать через х.
Появление ЭВМ кардинально изменило ситуацию. Класс математических моделей, допускающих подробное исследование, резко расширился. Решение многих, еще недавно недоступных, вычислительных задач стало обыденной реальностью.
Проверка качества модели на практике и модификация модели. На этом этапе выясняют пригодность математической модели для описания исследуемого явления. Теоретические выводы и конкретные результаты, вытекающие из гипотетической математической модели, сопоставляют с экспериментальными данными. Если они противоречат друг другу, то выбранная модель непригодна и ее следует пересмотреть, вернувшись к первому этапу. Если же результаты совпадают с допустимой для описания данного явления точностью, то модель можно признать пригодной. Конечно, необходимо дополнительное исследование с целью установления степени достоверности модели и границ ее применимости.
Вопросы для повторения:
1. Что такое математическая модель?
2. Основные этапы построения математической модели?
3. Основные типы решаемых задач?
2. Основные этапы решения инженерной
задачи с применением ЭВМ
Решение инженерной задачи с использованием ЭВМ можно разбить на ряд последовательных этапов. Выделим следующие этапы:
1) постановка проблемы;
2) выбор или построение математической модели;
3) постановка вычислительной задачи;
4) предварительный (предмашинный) анализ свойств вычислительной задачи;
5) выбор или построение численного метода;
6) алгоритмизация и программирование;
7) отладка программы;
8) счет по программе;
9) обработка и интерпретация результатов;
10) использование результатов и коррекция математической модели.
Постановка проблемы. Первоначально прикладная задача бывает сформулирована в самом общем виде:
— исследовать некоторое явление,
— спроектировать устройство, обладающее заданными свойствами,
— дать прогноз поведения некоторого объекта в определенных условиях и т. д.
На данной стадии происходит конкретизация постановки задачи. Первостепенное внимание при этом уделяется выяснению цели исследования.
Этот очень важный и ответственный этап завершается конкретной формулировкой проблемы на языке, принятом в данной предметной области. Знание возможностей, которые дает применение ЭВМ, может оказать существенное влияние на окончательную формулировку проблемы.
Выбор или построение математической модели. Для последующего анализа исследуемого явления или объекта необходимо дать его формализованное описание на языке математики, т. е. построить математическую модель. Часто имеется возможность выбора модели среди известных и принятых для описания соответствующих процессов, но нередко требуется и существенная модификация известной модели, а иногда возникает необходимость в построении принципиально новой модели.
Постановка вычислительной задачи. На основе принятой математической модели формулируют вычислительную задачу (или ряд таких задач). Анализируя результаты ее решения, исследователь предполагает получить ответы на интересующие его вопросы.
Предварительный анализ свойств вычислительной задачи. На этом этапе проводят предварительное (предмашинное) исследование свойств вычислительной задачи, выяснению вопросов существования и единственности решения, а также исследованию устойчивости решения задачи к погрешностям входных данных.
Выбор или построение численного метода. Для решения вычислительной задачи на ЭВМ требуется использование численных методов.
Часто решение инженерной задачи сводится к последовательному решению стандартных вычислительных задач, для которых разработаны эффективные численные методы. В этой ситуации происходит либо выбор среди известных методов, либо их адаптация к особенностям решаемой задачи. Однако если возникающая вычислительная задача является новой, то не исключено, что для ее решения не существует готовых методов.
Для решения одной и той же вычислительной задачи обычно может быть использовано несколько методов. Необходимо знать особенности этих методов, критерии, по которым оценивается их качество, чтобы выбрать метод, позволяющий решить проблему наиболее эффективным образом. Здесь выбор далеко не однозначен. Он существенно зависит от требований, предъявляемых к решению, от имеющихся в наличии ресурсов, от доступной для использования вычислительной техники и т. д.
Алгоритмизация и программирование. Как правило, выбранный на предыдущем этапе численный метод содержит только принципиальную схему решения задачи, не включающую многие детали, без которых невозможна реализация метода на ЭВМ. Необходима подробная детализация всех этапов вычислений, для того чтобы получить реализуемый на ЭВМ алгоритм. Составление программы сводится к переводу этого алгоритма на выбранный язык программирования.
Существуют библиотеки из которых пользователи из готовых модулей свои программы, либо, в крайнем случае, приходится программу писать с «нуля».
Отладка программы. На этом этапе с помощью ЭВМ выявляют и исправляют ошибки в программе.
После устранения ошибок программирования необходимо провести тщательное тестирование программы — проверку правильности ее работы на специально отобранных тестовых задачах, имеющих известные решения.
Счет по программе. На этом этапе происходит решение задачи на ЭВМ по составленной программе в автоматическом режиме. Этот процесс, в ходе которого входные данные с помощью ЭВМ преобразуются в результат, называют вычислительным процессом. Как правило, счет повторяется многократно с различными входными данными для получения достаточно полной картины зависимости от них решения задачи.
Обработка и интерпретация результатов. Полученные в результате расчетов на ЭВМ выходные данные, как правило, представляют собой большие массивы чисел, которые потом представляются в удобной для восприятия форме.
Использование результатов и коррекция математическое модели. Завершающий этап состоит в использовании результатов расчетов в практической деятельности, иначе говоря, во внедрении результатов.
Очень часто анализ результатов, проведенный на этапе их обработки и интерпретации, указывает на несовершенство используемой математической модели и необходимость ее коррекции. В таком случае математическую модель модифицируют (при этом она, как правило, усложняется) и начинают новый цикл решения задачи.
Вопросы для повторения:
1. Основные этапы решение инженерной задачи с использованием ЭВМ?
3. Вычислительный эксперимент
Создание математических моделей и решение инженерных задач с применением ЭВМ требует выполнения большого объема работ. Нетрудно заметить аналогию с соответствующими работами, проводимыми при организации натурных экспериментов: составление программы экспериментов, создание экспериментальной установки, выполнение контрольных экспериментов, проведение серийных опытов) обработка экспериментальных данных и их интерпретация и т. д. Однако вычислительный эксперимент проводится не над реальным объектом, а над его математической моделью, и роль экспериментальной установки играет оснащенная специально разработанной программой ЭВМ. В связи с этим естественно рассматривать проведение больших комплексных расчетов при решении инженерных и научно-технических задач как вычислительный эксперимент, а описанную в предыдущем параграфе последовательность этапов решения как один его цикл.
Отметим некоторые достоинства вычислительного эксперимента по сравнению с натуральным:
1. Вычислительный эксперимент, как правило, дешевле физического.
2. В этот эксперимент можно легко и безопасно вмешиваться.
3. Его можно повторить еще раз (если в этом есть необходимость) и прервать в любой момент.
4. В ходе этого эксперимента можно смоделировать условия, которые нельзя создать в лаборатории.
Заметим, что в ряде случаев проведение натурного эксперимента затруднено (а иногда и невозможно), так как изучаются быстропротекающие процессы, исследуются труднодоступные или вообще пока недоступные объекты. Часто проведение полномасштабного натурного эксперимента сопряжено с губительными или непредсказуемыми последствиями (ядерная война, поворот сибирских рек) или с опасностью для жизни или здоровья людей. Нередко требуется исследование и прогнозирование результатов катастрофических явлений (авария ядерного реактора АЭС, глобальное потепление климата, землетрясение). В этих случаях вычислительный эксперимент может стать основным средством исследования. Заметим, что с его помощью оказывается возможным прогнозировать свойства новых, еще не созданных конструкций и материалов на стадии их проектирования.
Существенным недостатком вычислительного эксперимента является то, что применимость его результатов ограничена рамками принятой математической модели.
Создание нового изделия или технологического процесса предполагает выбор среди большого числа альтернативных вариантов, а также оптимизацию по ряду параметров. Поэтому в ходе вычислительного эксперимента расчёты проводятся многократно с разными значениями входных параметров. Для получения нужных результатов с требуемой точностью и в приемлемые сроки необходимо, чтобы на расчет каждого варианта тратилось минимальное время.
Разработка программного обеспечения вычислительного эксперимента в конкретной области инженерной деятельности приводит к созданию крупного программного комплекса. Он состоит из связанных между собой прикладных программ и системных средств, включающих средства, предоставляемые пользователю для управления ходом вычислительного эксперимента, обработки и представления его результатов. Такой комплекс программ иногда называют проблемно-ориентированным пакетом прикладных программ.
Вопросы для повторения:
1. Достоинства вычислительного эксперимента по сравнению с натуральным?
2. Недостатки вычислительного эксперимента?
4. Простейшие методы решения задач
4.1. Поиск корня функции.
Метод деления отрезка по полам (метод Вилли).

Метод хорд (секущих).

Этапы построения математической модели
При построении математической модели системы можно выделить несколько этапов.
• 1-й этап.Постановка задачи. Этапу предшествует возникновение ситуаций или проблем, осознание которых приводит к мысли их обобщения или решения для последующего достижения какого-либо эффекта. Исходя из этого, объект описывается, отмечаются вопросы, подлежащие решению, и ставится цель исследования. Здесь необходимо уяснить, что мы хотим получить в результате исследований. Предварительно нужно оценить, нельзя ли получить эти результаты другим, более дешевым или доступным путем.
• 2-й этап.Определение задачи. Исследователь старается определить, к какому виду относится объект, описывает параметры состояния объекта, переменные, характеристики, факторы внешней среды. Необходимо познать закономерности внутренней организации объекта, очертить границы объекта, построить его структуру. Эта работа называется идентификацией системы. Отсюда выбирается задача исследования, которая может решать вопросы: оптимизации, сравнения, оценки, прогноза, анализа чувствительности, выявления функциональных соотношений и т.п.
Концептуальная модель позволяет оценить положение системы во внешней среде, выявить необходимые ресурсы для ее функционирования, влияние факторов внешней среды и то, что мы ожидаем на выходе.
Необходимость проведения исследования возникает из реальных ситуаций, складывающихся в процессе работы системы, когда они в чем-либо начинают не удовлетворять каким-либо старым или новым требованиям. Если недостатки очевидны и известны методы их устранения, то нет необходимости в исследованиях.
Исходя из задачи исследования, можно определить назначение математической модели, которая должна быть построена для исследования. Такие модели могут решать задачи:
· выявления функциональных соотношений, заключающихся в определении количественных зависимостей между входными фактора ми модели и выходными характеристиками исследуемого объекта;
· анализа чувствительности, заключающегося в установлении факторов, которые в большей степени влияют на интересующие исследователя выходные характеристики системы;
· сравнения, заключающегося в сопоставлении ограниченного числа альтернативных вариантов систем или же в сопоставлении нескольких предлагаемых принципов или методов действия;
· оптимизации, состоящей в точном определении такого сочетания переменных управления, при которых обеспечивается экстремальное значение целевой функции.
Выбор задачи определяет процесс создания и экспериментальной проверки модели.
Любое исследование должно начинаться с построения плана,включающего обследование системы и анализ ее функционирования. В плане должны быть предусмотрены:
· описание функций, реализуемых объектом;
· определение взаимодействий всех систем и элементов объекта;
· определение зависимости между входными и выходными переменными и влияние переменных управляющих воздействий на эти зависимости;
· определение экономических показателей функционирования системы.
-получить более полную характеристику системы и ее поведения;
-познать объективные закономерности ее внутренней организации;
-очертить ее границы;
-указать на вход, процесс и выход;
-определить ограничения на них;
-построить ее структурную и математическую модели;
-описать ее на каком-либо формальном абстрактном языке;
-определить цели, принуждающие связи, критерии действия системы.
На основе концептуальной модели можно построить факторную модель, которая устанавливает логическую связь между параметрами объекта, входными и выходными переменными, факторами внешней среды и параметрами управления, а также учитывать обратные связи в системе.
• 3-й этап. Составление математической модели. Вид математической модели в значительной степени зависит от цели исследования. Математическая модель может быть в виде математического выражения, представляющего собой алгебраическое уравнение, или неравенство, не имеющее разветвления вычислительного процесса при определении любых переменных состояния модели, целевой функции и уравнений связи.
Для построения такой модели формулируются следующие понятия:
Следующим этапом построения системы является формирование математической модели, включающее в себя несколько видов работ: математическую формализацию, численное представление, анализ модели и выбор метода ее решения.
Математическая формализация осуществляется по концептуальной модели. При формализации рассматривают три основные ситуации:
1) известны уравнения, описывающие поведение объекта. В этом случае решением прямой задачи можно найти реакцию объекта на заданный входной сигнал;
2) обратная задача, когда по заданному математическому описанию и известной реакции необходимо найти входной сигнал, вызывающий этот отклик;
3)математическое описание объекта неизвестно, но имеются или могут быть заданы совокупности входных и соответствующих им выходных сигналов. В этом случае имеем дело с задачей идентификации объекта.
При моделировании производственно-экологических объектов в третьей ситуации при решении задачи идентификации используется подход, предложенный Н. Винером, и известный как метод «черного ящика». В качестве «черного ящика» рассматривается объект в целом, вследствие его сложности. Так как внутреннее устройство объекта неизвестно, мы можем изучить «черный ящик», найдя входы и выходы. Сопоставляя входы и выходы, можно написать соотношение
Основой выбора метода математического описания является знание физической природы функционирования описываемого объекта достаточно широкого круга эколого-математических методов, возможностей и особенностей ЭВМ, на которой планируется проведение моделирования. Для многих рассматриваемых явлений имеется достаточно много известных математических описаний и типовых математических моделей. При развитой системе математического обеспечения ЭВМ целый ряд процедур моделирования можно осуществит с помощью стандартных программ.
Оригинальные математические модели можно написать на основе проведенных исследований систем и апробированных в реалы ной обстановке. Для проведения новых исследований такие модели корректируются под новые условия.
Численное представление модели производится для подготовки ее к реализации на ЭВМ. Задание числовых значений трудностей не представляет. Осложнения встречаются при компактном представлении обширной статистической информации и результатов экспериментов.
Основными методами преобразования табличных значений к аналитическому виду являются: интерполяция, аппроксимация и экстраполяция.
Следующим этапом построения является анализ полученной модели и выбор метода ее решения. Основой для вычисления значений выходных характеристик модели служит составленный на ее базе алгоритм решения задачи на ЭВМ. Разработка и программирование такого алгоритма, как правило, не встречают принципиальных трудностей.
Основную роль при разработке алгоритма поиска оптимальны решений играют характер факторов математической модели, чисуи критериев оптимальности, вид целевой функции и уравнений связи Вид целевой функции и ограничений определяет выбор одного и трех основных методов решения эколого-математических моделей:
· исследования при помощи численных методов;
· исследования алгоритмических моделей с помощью методов экспериментальной оптимизации на ЭВМ.
Аналитические методы отличаются тем, что помимо точного значения искомых переменных они могут давать оптимальное решение в виде готовой формулы, куда входят характеристики внешней среды и начальные условия, которые исследователь может изменять в широких пределах, не меняя самой формулы.
Численные методы дают возможность получить решение путем многократного вычисления по определенному алгоритму, реализующему тот или иной численный метод. В качестве исходных данных для вычисления используются числовые значения параметре объекта, внешней среды и начальных условий. Численные методы являются итеративными процедурами: для проведения следующего шага расчетов (при новом значении управляемых переменных) пользуются результаты предыдущих расчетов, что позволяет получать в процессе вычислений улучшенные результаты и тем самым находить оптимальное решение.
Свойства конкретной алгоритмической модели, на которой базируется алгоритм поиска оптимального решения, например ее линейность или выпуклость, могут быть определены только в процессе экспериментирования с ней, в связи с чем для решения моделей этого класса используются так называемые методы экспериментальной оптимизации на ЭВМ. При использовании этих метод производится пошаговое приближение к оптимальному решению на основе результатов расчета по алгоритму, моделирующему работу исследуемой системы. Методы базируются на принципах поиска оптимальных решений в численных методах, но в отличие от них все действия по разработке алгоритма и программы оптимизации выполняет разработчик модели.
Имитационное моделирование задач, содержащих случайные параметры, принято называть статистическим моделированием.
Заключительным шагом создания модели является составление ее описания, которое содержит сведения, необходимые для изучения модели, ее дальнейшего использования, а также все ограничения и допущения. Тщательный и полный учет факторов при построении модели и формулировке допущений позволяет оценить точность модели, избежать ошибок при интерпретации ее результатов.
· 4-й этап. Вычисления. При решении задачи необходимо тщательно разобраться с размерностью всех величин, входящих в математическую модель, и определить границы (пределы), в которых будет лежать искомая целевая функция, а также требуемую точность вычислений. Если возможно, то вычисления проводятся при неизменных условиях по несколько раз, чтобы убедиться, что целевая функция не изменяется.
· 5-й этап. Выдача результатов. Результаты исследования объекта могут выдаваться в устной или письменной форме. Они должны включать в себя краткое описание объекта исследования, цели исследования, математическую модель, допущения, принятые при выборе математической модели, основные результаты вычислений, обобщения и выводы.