Треугольник. Важные факты о высоте, биссектрисе и медиане

Определения

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

Теорема

В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Теорема

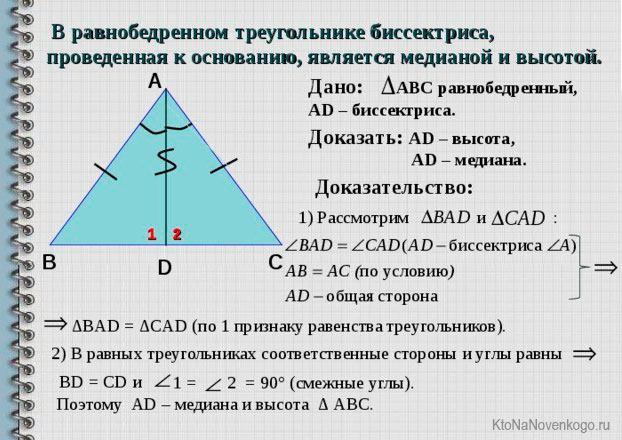
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

Доказательство

Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.

Теорема

Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).

Доказательство

Теорема

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.

Доказательство

Теорема

Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:

Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.

Доказательство

Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac>> = \dfrac = \dfrac\]

Теорема

Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.

Доказательство

Источник

Геометрия. 7 класс

Конспект урока

Медианы треугольника. Биссектрисы треугольника. Высоты треугольника

Перечень рассматриваемых вопросов:

Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.

Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Теоретический материал для самостоятельного изучения.

Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.

Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.

Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.

В любом треугольнике биссектрисы пересекаются в одной точке.

Введём понятие медианы треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BM – медиана треугольника ABC.

В любом треугольнике медианы пересекаются в одной точке.

Введём понятие высоты треугольника.

Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

AH – высота треугольника ABC.

В любом треугольнике высоты или их продолжения пересекаются в одной точке.

Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.

Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».

На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.

Докажем, что треугольники ABD и CED равны.

По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.

∠ADB = ∠CDE (по свойству вертикальных углов).

Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).

Что и требовалось доказать.

Разбор решения заданий тренировочного модуля.

В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.

1.Нарисуем рисунок по условию задачи.

2.По условию AD и BM – биссектрисы ∆ABC.

∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°

∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°

3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.

5.∠AOB = 180° – (25° + 40°) = 115°.

Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.

В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.

1.По условию ∠СОD = 90°.

Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.

2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.

3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.

Источник

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Треугольники

Виды треугольников

Треугольник называется равнобедренным, если у него две сторны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Треугольник, у которого все сторны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.

Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.

Основные линии треугольника

Медиана

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Биссектриса

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Высота

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

Срединный перпендикуляр

Свойства серединных перпендикуляров треугольника

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Формулы и соотношения

Признаки равенства треугольников

Два треугольника равны, если у них соответственно равны:

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны, если у них соответственно равны:

Подобие треугольников

Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия:

В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Формулы площади треугольника

Источник

Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком термине, как БИССЕКТРИСА.

Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.

Биссектриса — это.

Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.

Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.

Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:

Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».

Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.

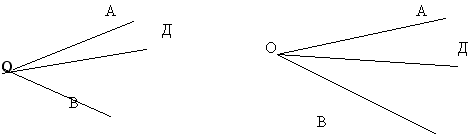
А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.

На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.

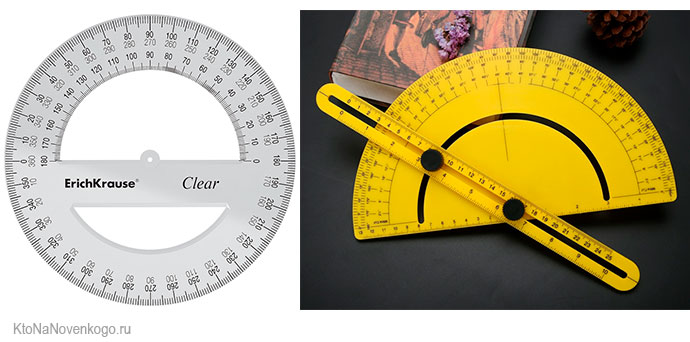
Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:

Хотя есть еще вот такие варианты:

Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.

И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.

Количество биссектрис в треугольнике

Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?

Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.

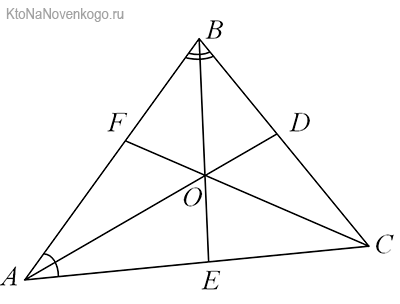
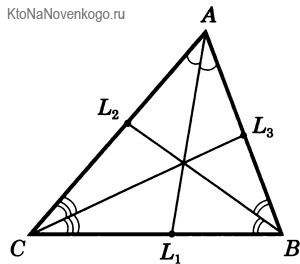
Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.

На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.

То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.

Пересечение биссектрис треугольника

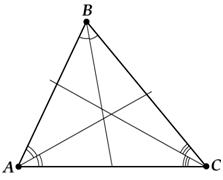
Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:

Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!

Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:

Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.

А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.

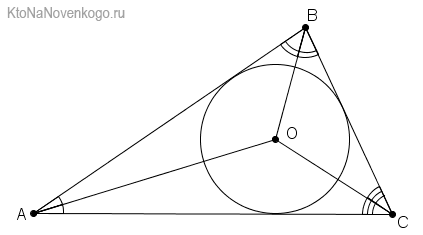
Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.

Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.

Свойство основания биссектрисы

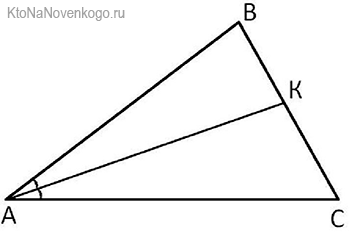
У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.

И с этим основанием связана одна весьма интересная теорема. Она гласит, что

Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.

Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:

Интересно, что для данной теоремы будет справедливо и другое утверждение:

Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.

Биссектриса равнобедренного треугольника

Для начала напомним, что такое равнобедренный треугольник.

Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).

Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.

Она одновременно является еще и медианой (что это?), и высотой.

Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:

А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.

Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.

Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.»

Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.

Математика требует точности. Спасибо.

При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.

Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.

Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.

Источник