Равнобедренный треугольник и равносторонний треугольник в чем разница
Геометрия. 7 класс
Конспект урока
Повторение. Равнобедренный треугольник и его свойства
Перечень рассматриваемых вопросов:
Треугольник называется равнобедренным, если две его стороны равны.
Треугольник называется равносторонним, если все его стороны равны.
Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противопложной стороны.
Теоретический материал для самостоятельного изучения.
Треугольник называется равнобедренным, если две его стороны равны.
Две равные стороны называют боковыми сторонами, а третью сторону – основанием равнобедренного треугольника.
Свойства равнобедренного треугольника:
В равнобедренном треугольнике углы при основании равны;
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Признак равнобедренного треугольника:
Если в треугольнике два угла равны, то он равнобедренный.
Равносторонний треугольник – треугольник, у которого все стороны равны.
Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противопложной стороны.
Разбор решения заданий тренировочного модуля
№ 1. Периметр равнобедренного треугольника равен 24 см, боковая сторона 10 см. Найдите основание.
Решение: ∆ABC равнобедренный, AB = BC = 10 см.
№ 2. ∆ABC равнобедренный. AM, CM биссектрисы, ∠B = 80°. Найти ∠AMC, который образуют биссектрисы углов при основании.
Треугольник — определение и основные свойства и виды треугольника
Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.
Определение треугольника
Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.
Посмотрите на треугольник на рисунке.
У него три вершины — 






будут звать 
По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.
В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.
Высота треугольника
В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.
Например, в треугольнике 

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.
В этом треугольнике три высоты 


Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.
Виды треугольника
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.
Виды треугольников по углам
В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный
, треугольник бывает остроугольным, тупоугольным или прямоугольным.
Посмотрите на рисунки — перед вами три основных вида треугольника:
Виды треугольников по сторонам
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.
На рисунке показаны равносторонний и равнобедренный треугольники.
Свойства сторон треугольника
Треугольник имеет важные свойства и характеристики.
Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.
Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.
Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:
Например, пусть наш треугольник имеет длины двух сторон 

Решение: согласно свойству сторон треугольника, получим:
Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.
Правило существования треугольника
Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.
Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.
Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?
Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.
Свойство углов в треугольнике
Сумма всех углов в треугольнике равна 
Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна 
Например, пусть известно, что в треугольнике 



Так как сумма углов в треугольнике равна 

Ответ: 
Элементы композиции
Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.
А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:
Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.
Виды треугольников
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).
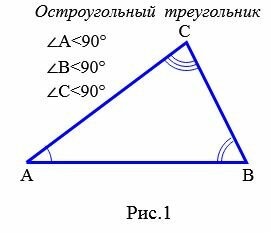 |
Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).
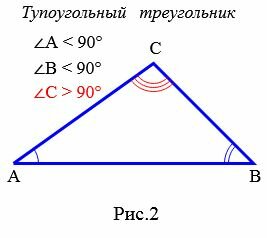 |
Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.
Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).
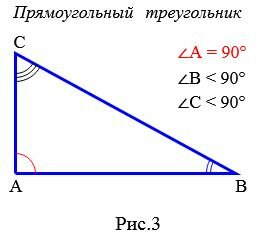 |
Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).
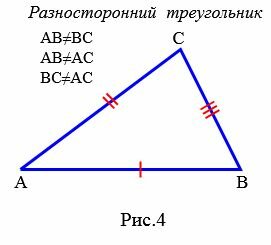 |
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).
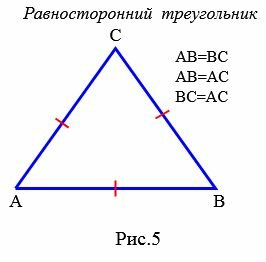 |
Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).
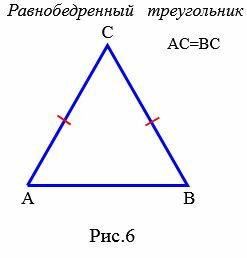 |
В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.
Гимназия 1503
четвёртый класс
И всё-таки она вертится…
Как хорошо, когда задача имеет несколько решений. Есть место для творчества.
Как поднимается настроение, когда решение задачи неявное и не лежит на поверхности. Можно выйти за рамки и почувствовать себя свободным.
На уроке математики у нас возникла дискуссия на тему — является ли равносторонний треугольник равнобедренным. Одни утверждали, что да, другие с ними спорили.
Пришлось обратиться к самым умным сайтам в интернете и побеспокоить дедушек с математическим образованием.
И вот что мы выяснили.
Определение: равнобедренный треугольник — это треугольник, в котором две стороны равны по длине.
Из определения равнобедренного треугольника следует, что правильный (равносторонний) треугольник также является равнобедренным.
Если взять длины сторон, как признак, и разделить треугольники по типам, то типы будут следующие: разносторонний, равнобедренный и частный случай равнобедренного — равносторонний.
Условие равенства двух сторон является необходимым и достаточным, чтобы считать треугольник равнобедренным.
Условие достаточности может выполняться и не выполняться в остроугольном, тупоугольном и прямоугольном треугольнике. Но в равностороннем треугольнике оно выполняется всегда.
Следовательно равносторонний треугольник всегда является равнобедренным.
Рассмотрим рисунок и вспомним определение.
АВ=ВС — следовательно, Δ АВС является равнобедренным (по определению).
ВС=СА — следовательно, Δ АВС является равнобедренным (по определению).
СА=АВ — следовательно, Δ АВС является равнобедренным (по определению).
Как видим, равносторонний треугольник АВС является не просто равнобедренным, а трижды равнобедренным.
Математика, которая мне нравится
Математика для школьников и студентов, обучение и образование
8. Равносторонний треугольник
Это не тест, не проверка Ваших знаний. Это приглашение к дискуссии. Выберите один из возможных вариантов и постарайтесь продолжить его, обосновывая Вашу точку зрения.
Является ли равносторонний треугольник равнобедренным?
• Не является, так как в равнобедренном треугольнике только две стороны равны
Комментариев: 16
1 Корнеев В.Ф.:
2 Корнеев В.Ф.:
Является, так как равносторонний т-к является частным случаем равнобедренного.
3 Лейб:
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине.
Naitkin Reply:
Октябрь 16th, 2014 at 17:06
По-моему, очень логичное и гармоничное с точки зрения математики и биологии;) определение. Бёдра всегда привлекали внимание ценителей математики и женщин;) (Y) Два бедра равной длины – красивейшее из образов:)
4 Корнеев В.Ф.:
Нравится. Нравится и всё. Равносторонний т-к является частным случаем равнобадренного.
5 zbl:
Равнобедренный треугольник — это треугольник у которого бёдра равны по величине.
Про третью сторону в определении ничего не говорится.
Поэтому равносторонний треугольник — это частный случай равнобедренного.
6 Вячеслав:
Равносторонний треугольник по определению не является равнобедренным, так как в равнобедренном треугольнике равны между собой только две стороны, а в равностороннем – все стороны равны между собой. Равносторонний треугольник является только частным случаем равнобедренного, но отличается от него. Чтобы построить равносторонний треугольник достаточно знать длину только одной стороны, а для построения равнобедренного надо знать длины двух сторон. Определение равнобедренного треугольника приведенное Лейбом абсолютно правильное.
Naitkin Reply:
Октябрь 17th, 2014 at 16:03
А=”Равносторонний треугольник по определению не является равнобедренным”
В=”Равносторонний треугольник является только частным случаем равнобедренного”,
Эти два выражения не могут быть истинны одновременно.
Вячеслав Reply:
Октябрь 18th, 2014 at 13:54
В реальности оба выражения истинны. Это наглядно видно из рисунка 7 vasil stryzhak. Всё множество треугольников равнобедренные, включая красный равносторонний, что соответствует выражению В. Но только один (красный) равносторонний является исключением из множества равнобедренных, и поэтому не может называться только равнобедренным. Для определения треугольника с равными сторонами недостаточно сказать, что он равнобедренный. Это особый вид, не являющийся только равнобедренным, и у него есть специальное название.
Naitkin Reply:
Октябрь 19th, 2014 at 9:36
“Только” равно бедренным, он (равносторонний) естественно не является. Но равнобедренным, он при этом является. Равносторонний треугольник “получается” из равнобедренного не теряя ни одного из свойств равнобедренного. А значит
C = “равносторонний треугольник является равнобедренным”, и
D = “равносторонний треугольник является частным случаем равнобедренного.”
это идентичные высказывания (C=D).
Приведи пример, какое свойство равнобедренный треугольник теряет (именно теряет! [Если приобретает, то все свойства равнобедренного в нём остаются]) и становится равносторонним?
(Только 2 стороны равны, напомню, это не свойство. Это из определения. А раз мы дискутируем об определениях как раз, то нам необходимо вообще абстрагироваться от определений. Не принимать во внимание определения вообще и понять что же такое равнобедренный и равносторонний треугольники. Выясним, какого же определение, зная только свойства.)
Вячеслав Reply:
Октябрь 19th, 2014 at 21:13
О каких свойствах можно говорить без определений? Разве равенство двух сторон в равнобедренном треугольнике следует не из его определения?. Почему нужно приводить пример свойства равнобедренного треугольника, которое он теряет, становясь равносторонним? Нельзя потерять то, чего не имеешь. Равнобедренный треугольник не имеет третьей равной стороны и этого свойства он потерять не может.
Naitkin Reply:
Октябрь 20th, 2014 at 23:00
Нельзя же доказывать определение (мы же именно его выясняем) с помощью самого определения!? По твоим рассуждениям, например, можно аналогично сказать, что квадрат не будет являться прямоугольником, а страус не будет являться птицей.
Naitkin Reply:
Октябрь 17th, 2014 at 16:17
Прошу прощения за неточность во второй картинке:
7 vasil stryzhak:
Naitkin Reply:
Октябрь 19th, 2014 at 9:44
Ваша картинка выражает мнение, что равносторонний треугольник является равнобедренным (по построению). Я вас правильно понял?
8 Naitkin:

Давайте рассуждать логически. Я нарисовал более общую схему всех треугольников, и отдельно привел только взаимоотношения равностороннего и равнобедренного. Случаев может быть только 3.
Либо случай 1, и тогда верно что никакой равносторонний треугольник не является равнобедренным.
Либо случай 2: всякий равносторонний треугольник является также и равнобедренным.
И может быть случай 3 (по Вячеславу): “Равносторонний треугольник является только частным случаем равнобедренного, но отличается от него.” В таком случае, должны найтись некоторые равносторонние треугольники, которые обладают свойствами равнобедренного, а некоторые другие равносторонние треугольники – не будут обладать свойствами равнобедренного. Что не может быть, т.к. не может быть Различных равносторонних треугольников. Варьировать в равностороннем треугольнике можно только размером, но независимо от размера, у всех равносторонних треугольников свойства одинаковые.
Теперь, рассмотрим случай 1: в этом случае равносторонний треугольник не должен обладать хотя бы одним из свойств равнобедренного (В равнобедренном треугольнике углы при основании равны; В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой; В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой; В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.) Однако, всеми этими свойствами равносторонний треугольник обладает. А значит его место, только с Случае 2. И равносторонний треугольник по праву может называться равнобедренным.



























